10月4日0時頃、緊急地震速報が発表された関係で、私が以前書いた「緊急地震速報」が小バズを起こしました。災害をきっかけにバズるというのは何とも複雑な気分ですが、とりあえず速報後に実際に来た地震は小規模なものだったので良かったです。
Twitterなどで拡散してくださった皆様、それを読んでわざわざ足を運んでくださった皆様、本当にありがとうございます。そして、日頃から当ブログを読んで下さっている方々もいつも本当にありがとうございます。
私が言いたいことは1つだけ。「あまり当ブログに書いてあることを信用するな」ということですw
コードを数えてみよう!
さて、今日はこんな売れないユーチューバーのようなアホ企画に挑戦してみたいと思いますw
コードは自分で勝手に作ることもできるし、そもそも時代や地域によって表記方法が異なるし、正確な個数を特定することはできませんが、とりあえず今回は、現実には絶対に有り得ない物も含め、私が考えつく限りのコードを数えてみたいと思います。
注:ただのネタ企画なので、数え方がおかしいぞ! などとマジレスをしないようお願いします
スポンサーリンク
3度・5度のバリエーション
まずCのコードを例に、3度の音にどのようなバリエーションがあるか考えてみましょう。
普通のCとCm、あとCsus4と、それからあまり使うものではないし、そもそも独立したコードとして考えていいのか微妙なところではありますがCsus2というものもありますね。
これらの4つのコードに対して、それぞれ(#5)と(♭5)が存在するので、4×3=12種類です。
Cm(#5)というコードはA♭/Cと構成音が一緒ですが、とりあえず表記方法が違うので独立してカウントしてしまいます。
テンション
次に、先程の12種類のコードに7thや9thなどの数字を付けてみましょう。(正確には、テンションとは9th以上の数字を指しますが…)
コードに付けられる数字は以下の10種類があります。

これらを組み合わせてテンションコードを作っていくわけですが、基本的には一つの数字は一回しか使えません。例えばC7M7とか、C(9 , ♭9)などというコードは存在しません。
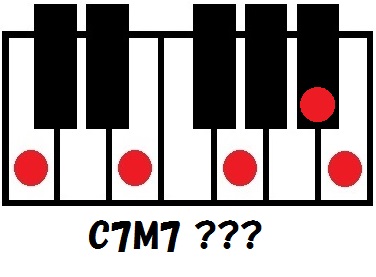
しかし今回はこういったコードも全部カウントしてしまいます。
上の図のような和音が世の中に存在しない、これから先の未来においても絶対に使われることはない、などとは断言できません。可能性がある以上はカウントします。
ではカウントしていきましょう。
まずC Cm Csus4 Csus2のコード、これは先程紹介したテンションのうち、9種類を使うことができます。(なぜ10種類ではないのかと言うと、例えばCのコードはミの音が♭11thのテンションと共通のため使えないから)
9種類のテンションの中からどれか1つを選ぶ組み合わせは、当然9パターン。どれか2つを選ぶ組み合わせは、36パターンあります。
…え、2つ選ぶと36になる理由が分からない?
え~っと、数学で習った「コンビネーション」という計算ツールを思い出して下さい。9つの物の中から2つを選ぶ組み合わせパターンは「9C2 = 36」という式で求めることができます。
ここは数学を解説するブログではないので先に進みますが、同様の計算をすると、3種類選ぶときは84パターン、4種類だと126パターン、5種類だと126パターン、6種類は84パターン、7種類は36パターン、8種類は9パターン、9種類は1パターンです。
一つのコードにつき、付けられるテンションは合計511パターン。よってC、Cm、Csus4、Csus2のそれぞれについて考えると511×4=2044種類。
次に、C(#5) C(♭5) Csus4(#5) Csus4(♭5) Csus2(#5) Csus2(♭5) Cm(#5) Cm(♭5)の8種類について考えてみましょう。これらのコードは、使えるテンションが8種類です。
10種類全部使えるわけではない理由は先程と同様。例えばC(#5)のコードはミの音が♭11thのテンションと共通で、ソ#の音が♭13thのテンションと共通だからです。
これも先程と同様に計算いていくと、1種類選ぶ組み合わせは8パターン、2種類だと28パターン、3種類は56パターン、4種類は70パターン、5種類は56パターン、6種類は28パターン、7種類は8パターン、8種類は1パターンです。
一つのコードにつき合計255パターンなので、それぞれについて考えると255×8=2040種類。
6th
残念なお知らせです。こいつの存在を忘れておりました…。
6thは通常、C69のように9thとセットで使われることがたまにありますが、それ以外のテンションと組み合わさることはまず有り得ません。しかしこれも考えうる限りはカウントしてしまいましょう。
カウント方法はそれほど難しくはありません。6thの音は13thと共通なので、先程計算したそれぞれのコードについて使えるテンションが一個ずつ減るだけです。
C6 Cm6 C6sus4 C6sus2については、使えるテンションが8種類になるので、255×4=1020種類。
C6(#5) C6(♭5) C6sus4(#5) C6sus4(♭5) C6sus2(#5) C6sus2(♭5) Cm6(#5) Cm6(♭5)については、使えるテンションが7種類になるので、127×8=1016種類。
dim
続いてdimです。これは書き換えるとCm6(♭5)と考えることができるので、既にカウントは済んでいるのですが、一応表記方法が違うということで再度カウントしてしまいましょう。
1オクターブは12音、dimは4和音なので、残りの8音全てテンションとして使えそうですが、ソの音を表すテンションは現状表記が確立されていないので、使えるテンションは7音として考えましょう。
合計127種類です。
合計は…
さて、ここまでの合計は、何と6259種類です!
今まで全てCをルートとして考えてきましたが、これに対してC# D D#…と、12種類のルートが考えられるので「×12」。さらに、それぞれのコードに対して分数コードが考えられるので、さらに「×12」です。
最終的な数字は、
6259×12×12=901296
考えうるコードの種類は、90万1296個です!
いかがでしょうか。う~ん、私個人的には100万以上は軽く行くと思っていたのでちょっと少なく感じますね。
現実的に有り得るのはこの中の10分の1程度でしょうから、9万個といったところです。実際の曲中で使われるコードは、さらに10分の1程度で9千個ぐらいでしょうか。
90万という数字は、全然正確なものではありません。冒頭で言ったように、そもそもコードの数を正確にカウントすることなどできません。計算方法次第ではこれより多くもなるし少なくもなります。
例えば私の計算方法だと、CdimとCm6(♭5)を別物として二重でカウントしていますが、C#とD♭は二重カウントしていません。この辺りの計算方法が変われば、結果は全く違ったものになるでしょう。
また、現在のコード表記法では、12度の音や15度以上の音を表す方法が存在しませんし、「ド ド# レ」のような和音を表す方法もありません。将来的にこれらの表記方法が確立されれば、数はもっと増えるでしょう。
さて、今回のアホ企画いかがでしたでしょうか。いきなりこんな企画に挑戦するのはネタが尽きかけている証拠ですねw
非常にややこしい計算だったので途中で間違えているかもしれませんし、意外なコードが抜けている可能性もあります。
間違いに気づいた方がいらっしゃいましたら、是非ご自分で計算し直してみてください。