昔々、古代ギリシアのピタゴラスが鍛冶屋の前を通りかかったとき、2人の鍛冶屋が振り下ろすハンマーの音が綺麗にハモるときとハモらないときがあることに気づきましたとさ。
色々と研究してみたところ、2つのハンマーの重さが「2:1」「3:2」「4:3」のような、簡単な整数比のときに綺麗な協和音程を奏でることが判明したんだとさ……
2音の比
えっと、冒頭から恐縮ですが、残念なお知らせが2つあります。
まず、固有振動数とは重さにそのまま(2倍なら2倍、3倍なら3倍といった単純な感じで)比例するものではないので、このエピソードは嘘です。
それと、ピタゴラスは弟子達の発見も自分の名前で発表していたので、この法則、或いはこれから紹介する音律も、どうせピタゴラス本人ではなく弟子の発見だろうと私は思っています。
まぁともかく、この「比」を利用して音高・音階を定義するのがピタゴラス音律です。
現代の知識で言うと、弦の長さが半分、つまり元の弦に対して2:1の長さを持つ弦は、元の弦のオクターブ上の音が出ますね。
同様に、元の弦に対して3:2の長さの弦は5度上、4:3の長さの弦は4度上です。
確かに、これらの音は全部よく協和しますよね。ピタゴラスさんはこれを発見したわけです。
ギターやベースを持っている人は、実際に測ってみましょう。
12フレットの位置は、開放弦の丁度真ん中(半分の長さ)にあるはずですよ。
スポンサーリンク
これが本当の「連続5度」
この考え方を拡大させていくとどうなるでしょうか。
例えば、Cの音が出る弦があるとしましょう。この弦に対して3:2の長さを持つ弦は5度上、つまりGの音が出ます。
このGの弦に対してさらに3:2の長さを持つ弦を用意します。するとこの弦の音はGの5度上なのでDの音が出ます。

このままだとDの音が若干高いので、弦の長さを2倍にしてオクターブ低くしましょう。

はい、丁度いい配置になりました。
では実験を続けましょう。
D弦に対して3:2の長さの弦はA音。
A弦に対して3:2の長さの弦はE音。これも若干高いのでオクターブ下げます。

以下、同様にB→F#(オクターブ下げ)→C#(オクターブ下げ)→G#→D#(オクターブ下げ)→B♭→F(オクターブ下げ)→C

おっと、一旦ストップ!
ついに「最初の音(C)ととてもよく似た音」が現れました。
これ以降もまた同じ音(G→D→…)が現れますから、弦の長さを3:2にする作業はここで終了です。
登場した音を数えると、全部で12種類あります。
1オクターブが12音なのは、これに由来しているんですね!
次のCが登場するまで100音あったら、1オクターブは100音になっていたのでしょうか…。
パラドックス
さて、これで一件落着かと言うと、実は全然違います。
今、弦の長さを3:2、つまり2/3にして、さらに少々高い音は弦の長さを2倍にしてオクターブ下げることで音階を定めましたね。
周波数(Hz)で言うと、周波数は弦長の逆数に比例するので、弦長2/3は「×3/2」で、弦長2倍は「×1/2」です。
つまり次のCが登場するまでに、最初のCに「×3/2」を12回、それから「×1/2」を6回行ったのです。
計算すると、

あれ…何で…???
オクターブ上の音は周波数が2倍になるはずなのに、何か中途半端な数になってしまいました。放送事故だ!

考えてみれば当然です。2と3を組み合わせて2を作れるはずがありません。
上の式を満たす整数mとnは存在しないのです。
異名同音?
でも、オクターブ上の音は周波数が2倍だと自然科学的に決まっているのだから、計算上それがちゃんと求められないのは変ですよね。
一体なぜこんなことが起こるのでしょうか。
先程弦長を3:2にして音階を導いたとき、私は音階の最後のほうを「D#→B♭→F→C」と表記しました。
実はこれが間違いなのです。
だってよく考えてみて下さい。
Dの5度上の音ってAですよね。だったらD#と協和する5度上の音って、B♭じゃなくてA#じゃないですか!
同様に、A#と協和する5度上の音はFではなくE#です。
ということは、最後の音はCではなくB#なのです。
ピアノやギターではCとB#は同じ音ですが、ピタゴラス音律では違う音です。
「C#とD♭」や「D#とE♭」なども全て異なる音です。
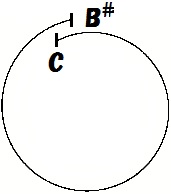
これが先程のズレの原因です。
オクターブ上の音を求めているようで、実は違う音に到着してしまったのです。
ちなみに「CとB#」や「C#とD♭」などの音高の差は約23.5セント。
半音が100セントなので、だいたい半音の4分の1程度の違いがあるわけです。
この23.5セントの差をピタゴラスコンマ(ピタゴラスカンマ)と言います。
実際に半音の4分の1ズレたオクターブの音を聞いてみましょう。
う~む、ホンキートンク感が凄いw
これはこれで有りだと思いますが、当然ながら古代ギリシアにラグタイムは存在しないので、ピタゴラス的には無しです。
この唸りはオクターブだけでなく5度(FとB#)でも発生し、後世(中世ヨーロッパ)の人々はこれをオオカミの吠声に例えて「狼の5度」(ウルフインターバル)と呼びました。
何でいきなりオオカミやねん…と思うところですが、おとぎ話の悪役としてよくオオカミが登場するように、中世ヨーロッパではオオカミは外敵・異教徒の象徴だったからでしょう。
日本で言えば「カラスの5度」「黒猫の5度」みたいなもんですかねw
話を戻しましょう。
その「狼の5度」を回避するためには一体どうすればいいかと言うと、あまり使わない音(A♭とか)から調律を始めればいいのです。
A♭→E♭→B♭→F→C→G→D→A→E→B→F#→C#→G#
こうすれば、とりあえず「C D E F G A B」は問題なく使えます。
「A♭とG#」や「E♭とG#」は不協和音になりますが、そういう音は使わないように作曲すればいいのです。
3度は不協和音
後世の人間から見たピタゴラス音律のデメリットはもう一つあって、それは長3度音程が広いため、ドとミなどが美しく響かないとされることです。
計算上、長3度の理想的な周波数比は5/4なのですが、ピタゴラス音律では81/64です。

う~ん…確かに広いけど、不協和音と言う程では…。
しかし、時代が流れて音楽の発展とともに長3度和音が使われるようになると、当時の人々はこの広さが妙に気になったらしく、それが純正律の開発に繋がりました。
三分損益法
ちなみに古代中国では三分損益法という音律が発明されており、これは「ある長さの弦(管)の3分の1を切ると5度上の音が出て、3分の1長くすると4度下の音が出る。この操作を繰り返して音階を導く」という、ピタゴラス音律の考え方と同じものです。
というわけで、次は純正律について見てみましょう。