リディアン・クロマティック・コンセプト後編です。
前編「リディアン・クロマティック・コンセプト 前編」ではLCCの基本的な考え方について学びました。後編ではアドリブからは一旦離れて、より広い考え方を勉強しましょう。
コードや調の距離
5度圏上の距離は、コードや調の相性にだいたい相当します。

例えば、Cの近所にはFやGがあるので、C(コードや調)は、FやG(コードや調)とは自然に連結することが出来ます。
一方、F#などは遠い位置にあるので、CとF#の連結はなかなか違和感があります。
この考え方はLCCでも同じです。
ではここで復習です。「C→Dm→G7→C」という進行で、それぞれのコードのペアレント・スケールは何リディアンでしょうか。
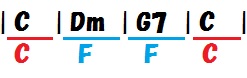
前編の内容が理解できている方には超簡単。CはCリディアン、DmとG7はFリディアンですね。
つまりLCC的には、「C→Dm→G7→C」とは「Cリディアンから始まり、一旦Fリディアンに行き、またCリディアンに戻ってくる」という進行であると考えられます。
先程見たように、5度圏上ではCとFは近親関係にありますから、この「C→Dm→G7→C」という進行は、その観点からも自然な連結であると言えます。
もちろん、リディアン以外のスケールでも同様です。
例えばD♭7(#5) というコードは、Fリディアン・オーギュメントがペアレント・スケールとなります。
となると「C→D♭7(#5)」というコードの連結も、結局は「C→F」という連結になりますから、近親関係にあると言えます。なんか不思議ですねw
(本当はこれも一覧表が載っていて、それを元にペアレント・スケールを探します)
通常のコード進行同様、遠くへ行くのが駄目という訳ではありません。 時には意表を突いて遠いコードに行くことも大事ですが、何が遠くて何が近いのか、その距離の目安・基準になるのがこの考え方だということです。
ただしこの考え方もなかなか微妙な点があり、例えば A♭7 は G♭リディアン がペアレント・スケールなので、「C→A♭7」という進行は、5度圏上で最も遠い進行となります。
しかし「C→A♭7(#5)」になると、Cリディアン・オーギュメントがペアレント・スケールなので、「C→C」で最も近い進行となってしまいます。
スポンサーリンク
調性引力
ある一つの音と、それ以外の11音との遠近感系を順位付けする考え方を「調性引力(Tonal Gravity)」と言います。
gravityは一般的には重力と訳されますが、「重さ」「重大さ」のような意味もあるらしいので、単純に「音の近親関係」のようなニュアンスだと思ったほうが良いでしょう。
ある音の5度上の音を次々取っていった場合、ファより先にファ#が登場します。例えばCから順番に「C→G→D→A→E→B…」と5度上の音を取ると、次にF#が登場し、Fはかなり最後の方まで出てきません。
なぜ5度上の音を次々取るのかと言うと、ピタゴラス音律に倣ったからです。ジョージ・ラッセルは、これが紀元前から続く西洋音楽の伝統であると言っています。
また、下の2つの和音を比べてみましょう。
どちらのほうが一体感や終止感を持っているでしょうか。前者は長音階で、後者はリディアンから作られた和音ですね。
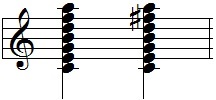
欧米で様々な人に聞き比べてもらったところ、多くの人が後者を選んだそうです。
これらが、LCCでリディアンスケールを用いる理由です。理論的にも聴覚的にもリディアンのほうが自然だということです。
さて、LCCでは次のような順列を用います。
C→G→D→A→E→B→F#→G#→D#→A#→F→C#
これが、Cという中心音に対して、残りの11音との遠近関係を順列化したものです。LCC的に言うと、左側にある音はインゴーイング、右側にある音はアウトゴーイングということです。
しかしよく見て下さい。なんか変ですね。
8番目に来るはずのC#が、なぜか最後尾に来ています。これに対してLCCでは「この順番でないと和声の歴史と矛盾する」という苦しい説明をしています。
つまり上の順列は、C音に対する大体の協和度を表しているわけです。左の方にある音はC音と相性が良いけど、右の方にある音は相性が悪い。
音楽の歴史的に、最初にメジャーコード(CGE)が出来て、次にマイナーコード(CAE)が出来て、セブンスコード(CDAF#)が出来て…と、左側にある音を使った和音ほど原始的。右側にある音を使った和音ほど近代的なのです。
さらに、前編で紹介した7つのスケールも、実はこの順列に則って作られています。
先程チラッと触れましたが、左側の7音を使ったスケールはリディアンですよね。次に、G音の代わりに8番目の音であるG#を使うと、リディアン・オーギュメント・スケールが出来上がります。同様に、9番目の音であるD#を使うと、リディアン・ディミニッシュ・スケールが出来上がります。
このように、順列内の音を左から一つずつ拾っていくことで、前編で紹介した7つのスケールを全て順番に作成できるのです。
これらの理由から、調性引力はあの順列でなくてはいけないのです。
まぁ言いたいことは分からなくはないのですが、C#音を最後尾に移動させることが許されてしまうのならば、F音を最初の方に移動させることも許されるはずです。
伝統という言葉を使う割にはけっこう適当なんだよなぁ…。
しかも、さっきの5度圏の話のときは、FはCの隣にあったしねw
ポリコード
最後にこれを解説して終わりにします。これはLCCの中で私が唯一「使える!」と思った理論ですw
ポリコードとは、簡単に言えばコードの上にもう一つコードを乗せた形のことです。
Cの上にDを乗せるとか、Amの上にGmを乗せるとか。一応3つ以上重ねてもいいのですが、一般的には2つです。
詳しく知りたい方はこちら「ポリコードとUST」をご覧ください

このポリコードを作る際の判断基準としてLCCが使えるというわけです。
例えばEm7というコードがあるとしましょう。Em7のペアレント・スケールはGリディアンです。

この場合、Em7の上にはGリディアン、或いは他の、Gをルートとする補助スケールを使って作れるあらゆるコードを乗せることが出来るというわけです。バーティカルスケールだけでなく、ホリゾンタルスケールも使えます。
例えばF#7というコードはG補助ディミニッシュを使って作ることが出来ます。よってこのコードはEm7の上に乗せることが出来ます。

「スケールは沢山あるのだから、乗せられないコードなんて無いんじゃないの?」と思うかもしれませんが、例えばF7やFm7、それからA♭7やA♭m7などは作れません。
LCCの解説は以上です。
武満徹はこの理論を絶賛したそうですが、一体どこに共感したのかよく分かりませんねw
ジョージ・ラッセルはもう亡くなっているようなので、残念ながら私がLCCの真意を理解することは一生なさそうです。