今日のテーマは、ピッチクラスセット理論です。
「セット」「ピッチセット」など、他にも様々な言い方があるようです。
12音技法「12音技法について」と同様、無調音楽体系化に対するアプローチの一つです。
アレン・フォート著「無調音楽の構造 ピッチクラス・セットの基本的な概念とその考察」に書かれている理論なのですが、残念ながら楽天では扱っていないようなので表紙の画像のみでご容赦くださいw

音程
まずピッチクラスとは、ド音を0として、そこから半音ごとに1 , 2 , 3…と番号を振ったものです。
「音程」の発展形と言えるかもしれません。

この番号は異名同音に対しても同様です。
例えばシ#やレのダブルフラットも0番だし、ミ♭も3番となります。
オクターブ上のドから先は、また0 , 1 , 2…となりますが、移高を分かりやすくしたい場合などは、稀に12 , 13 , 14…と書くこともあります。
また、12進数にするために10 , 11をA , Bと書く人もいます。
この数字の集合体を「ピッチクラスセット」と言います。
例えば「ドミソ」は [0 , 4 , 7] と表し、「ドレミファソラシ」は [0 , 2 , 4 , 5 , 7 , 9 , 11] と表します。
ピッチクラスセットを利用して作曲する手法のことを「ピッチクラスセット理論」というわけです。
普通(?)の音楽は、まず動機を用意して、その高さを変えたりリズムを変えたり、展開しながら曲を作っていきますよね。

ピッチクラスセット理論も同様で、用意したセットを色々と展開しながら無調音楽を作っていきます。
無調音楽は訳が分からないため、どのように作ればいいか困ってしまいますが、これにより簡単に作れるようになるのです。
では一体どのような展開が可能なのか勉強しましょう。
スポンサーリンク
同等なセット
あるセットを移高したり反行させたものを、元のセットと同等であると言います。

1小節目の旋律は [4 , 5 , 7 , 10]。また、2小節目の和音は [8 , 9 , 11 , 14] です。
つまり、1小節目の旋律に使われている音を移高(移置)すると2小節目の和音となるため、これらは同等であると言えます。
上の譜例では、片方が旋律で片方は和音です。
普通の音楽では、このようなペアは仲間であるとは考えられません。
しかしピッチクラスセット理論は数字だけに着目するため、このようなペアでも同等となります。
転回したセットについても同じことが言えます。
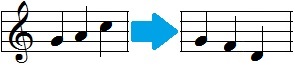
上譜例の2つの音型は、ソを基準として音程が逆になっています。左のセットは [7 , 9 , 12] で、右のセットは [7 , 5 , 2] ですね。
この [7 , 5 , 2] のようなセット、もしくはこれを移高した [8 , 6 , 3] などは、元のセットと「転回により同等である」と言います。
但し、上譜例のように「ソファレ」という旋律になっていれば転回形であるとすぐ分かるのですが、実際には順番が変わったり和音の形になってしまったりするため、これが元のセットの転回形であると気付くのは至難の業……
サブセット
あるセットAに包含されるようなセットBを「サブセット」と言います。
例えばAが [0 , 1 , 2 , 3 , 4] で、Bが [0 , 1 , 2] とか [3 , 4] とか [0 , 2 , 4] のようなセットだった場合、BはAに対するサブセットです。
数学で言うと A⊃B の状態ですね。
さらに、A [0 , 1 , 2 , 3 , 4]、B [0 , 2 , 4 , 6 , 8] というセットがあった場合、このAとBの共通部分 [0 , 2 , 4] を「共通音サブセット」と言います。

補集合
A [0 , 2 , 4 , 6 , 8 , 10] というセットに対して、[1 , 3 , 5 , 7 , 9 , 11] のセットをAに対する補集合とします。
数学の補集合と全く一緒ですね。
また、先程言ったように移高・転回したセットは元のセットと同等に扱うので、[1 , 3 , 5 , 7 , 9 , 11] を移高・転回したものもまたAに対する補集合と言って構わないようです。
以下、補集合を「アルファベットの上にバー」で表しますが、ブラウザによっては見づらくなってしまうようです。
ご容赦ください。
セット複合体
最後にちょっと応用編を説明して終わりにします。
セットAまたはĀがセットBまたはB̄の要素であるとき、「AはBのセット複合体メンバーである」と言うようです。
「メンバー」という言い方がとてつもなくダサイ……
数学記号で正式にどのように表記するのかは分かりませんが、冒頭で紹介した書籍には次のような式が書かれています。(説明を簡単にするために一部表記を変えています)

ちょっと分かりにくいので、iff以降を一つ一つ考えてみましょう。
A⊃Bのとき、Ā∈B̄
A⊂Bのときは明らかに成り立つ
A⊃B̄とき、Ā∈B
A⊂B̄のときは明らかに成り立つ
なるほど、確かに式は問題なく成り立っているようですね。
この4つの条件のうち、どれか1つを満たす関係にある2つのセットを「セット複合体メンバー」と言うようです。
毎度お馴染みですが、移高や転回の上で満たしてもOKです。
例えばA [0 , 1 , 2 , 3 , 4 , 5 , 8] と B [0 , 1 , 2 , 3 , 5 , 6 , 8 , 9] という2つのセットについて考えてみましょう。
これらは、「A⊃B」「A⊂B」「A⊂B̄」は満たしませんが、3番目の「A⊃B̄」については、B̄を転回(8 , 5 , 2 , 1)した場合に成り立ちます。
よって、AはBのセット複合体メンバーであると言えます。
しかし、4つの条件のうちどれか1つを満たせばいいだけなので、セット複合体メンバーであるセットを見つけることはそれほど難しくありません。
けっこう何でも該当してしまうので、これではグチャグチャに作っているのとあまり変わらない。
副複合体
そこで、「副複合体」についても考えてみましょう。
これは以下のような関係です。
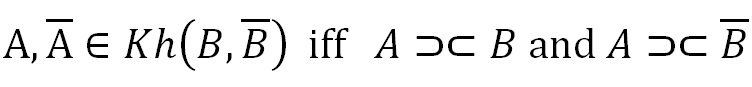
Khは「副複合体」を表す記号で、先程のK同様あまり意味はありません。
つまり先程の式との違いは、orがandになっていることだけですね。
例えばA [0 , 1 , 2] と B [0 , 1 , 2 , 3] は「A⊂B」と「A⊂B̄」を同時に満たします。
よってAはBの副複合体メンバーであると言えます。
2つの条件を同時に満たさなければいけないため、この関係にあるセットは先程よりもレアです。
このように、様々な形でセットを変形させたり、近親関係にあるセットを用いながら無調音楽を展開させていくのがピッチクラスセット理論です。
他にも色々なテクニックがあるのですが、本の文章が非常に分かりにくく、私には理解できませんでしたw
今回の解説は以上です。
ちなみに12音技法により作られた音列は、3音のピッチクラスセットが4つ集まったものだと考えられ、それぞれのピッチクラスセットは互いに同等であるらしいです。
面倒なので私は証明する気になりませんが、誰か挑戦してみてw